Решения
1. Для нахождения второй радуги, воспользуемся нашей формулой при $k=2$, так как в четвертой компоненте происходит два отражения. Получаем:
\begin{equation} \alpha^* = \mathrm{arctg}\sqrt{\dfrac{9-n^2}{n^2-1}} \end{equation}
Подставляем показатели преломления:
\begin{equation} \text{красный:} \quad n=1{,}331 \qquad \alpha^* = 71{,}91^\circ \qquad \theta^* = 230{,}4^\circ \end{equation}
\begin{equation} \text{синий:} \qquad n=1{,}343 \qquad \alpha^* = 71{,}52^\circ \qquad \theta^* = 233{,}5^\circ \end{equation}

Обратите внимание, углы поворота получились больше $180^\circ$, но все-таки ближе к $180^\circ$, чем к $360^\circ$. Это означает, что радуга будет наблюдаться в полусфере противоположенной Солнцу. Угол $\theta^*$ для красного цвета ближе к $180^\circ$, чем для синего. Это означает, что красная полоса радуги находится внутри, а синяя снаружи. И наконец, полученные нами углы для второй радуги немного дальше от $180^\circ$, чем углы для первой радуги. И правда
\begin{equation} |\theta^* - 180^\circ| \approx 52^\circ \end{equation}
Поэтому вторая радуга больше, то есть располагается снаружи от первой радуги. Кстати, и ширина ее тоже больше.
Почему мы почти никогда не видим вторую радугу? Просто ее интенсивность на небе гораздо меньше, чем у первой радуги. Для точной оценки интенсивности нужно учесть множество факторов, например, размер (площадь) радуги и зависимость коэффициентов отражения и пропускания света от угла падения. Но главная причина слабой интенсивности второй радуги — это дополнительное отражение внутри капли. Формулы Френеля, которые позволяют точно рассчитать, столько света отражается от границы раздела двух сред говорят: лишь примерно $14\%$ света отражается в рассматриваемом нами случае. Этот множитель делает вторую радугу гораздо менее интенсивной.
$\,$
2. Используем формулу при $k=1$ и данных показателях преломлени. Для серной кислоты получам: \begin{equation} \mathrm{H_2SO_4:} \qquad n= 1{,}43 \qquad \alpha^* = 54{,}0^\circ \qquad \theta^* = 150^\circ \qquad |\theta^* - 180^\circ| = 30^\circ \end{equation}
следовательно на Венере радуга должна быть меньше (по радиусу) чем на Земле (у воды радиус радуги — $42^\circ$).
А для метана: \begin{equation} \mathrm{CH_4:} \qquad n= 1{,}29 \qquad \alpha^* = 62{,}2^\circ \qquad \theta^* = 131^\circ \qquad |\theta^* - 180^\circ| = 49^\circ \end{equation}
следовательно на Титане радуга должна быть большее (по радиусу) чем на Земле.
$\,$
3. Если заменить воду на воздух, а воздух на воду, то показатель преломления воды $n=1{,}33$ переместится в законе Снелла на другую сторону равенства. Такого же эффекта можно добиться заменив его обратным числом, то есть используя в формулах $n=1/1{,}33=0{,}75$. Точка минимума функции $\theta(\alpha)$ равна
\begin{equation} \alpha^* = \mathrm{arctg}\sqrt{\dfrac{(k+1)^2-n^2}{n^2-1}} \end{equation}
Видим, что знаменатель подкоренного выражения отрицателен, значит числитель тоже должен быть отрицательным. Если $k=0,1,2,\ldots$ это невозможно, значит во всех компонентах рассеяния начиная со второй свет размазывается по направлениям более-менее равномерно.
Однако в первой компоненте, когда $k=-1$, подкоренное выражение оказывается положительным и мы можем получить стационарную точку
\begin{equation} \alpha^* = \mathrm{arctg}{\dfrac{n}{\sqrt{1-n^2}}} \end{equation}
Но это неверно! Действительно, при $k=-1$ функция $\theta(\alpha)$ равна $2\alpha-180^\circ$ и, очевидно, не имеет стационарных точек. Где мы допустили ошибку? Дело в том, что при этой $\alpha$ аргумент арксинуса в формуле для функции $\theta$ равен $1$. В этой точке арксинус не имеет производной, точнее производная бесконечна. Она умножается на $(k+1)=0$, что приводит к неопределенности. Если бы мы лучше следили за тем, в каких точках функция $\theta(\alpha)$ определена и дифференцируема, мы бы не допустили этой ошибки.
Ответ: нет, радуга на пузырьках воздуха в воде не образуется.
$\,$
4. Первый способ (тупой). Уравнение движения такого тела:
\begin{equation}
y(t) = v_ot-\tfrac{1}{2}gt^2
\end{equation}
Если известна высота $y$, то из него можно найти $t$:
\begin{equation}
t = \frac{v_o \pm \sqrt{v_o^2-2gy}}{g}
\end{equation}
Подставляя в эту формулу данные в задаче высоты мы получим, что впервые на этих высотах тело побывает в такие времена
\begin{array}{c|c}
высота, м & время, с \\
\hline
3{,}99 & 0{,}5506 \\
4{,}00 & 0{,}5528 \
4{,}99 & 0{,}9553 \
5{,}00 & 1{,}0000 \
\end{array}
Мы рассмотрим только движение тела вверх, так как движение вниз полностью симметрично. Тогда на первом промежутке высот тело пробудет всего $0{,}0022\,\text{с}$, а на втором промежутке высот целых $0{,}0447\,\text{с}$.
Второй способ (умный). Воспользуемся производными по их прямому назначению. По определению производной \begin{equation} \Delta y \approx \dot{y}(t)\Delta t \end{equation}
Следовательно, чтобы найти время $\Delta t$, необходимое на преодоление расстояния $\Delta y$, надо поделить его на производную $\dot{y}(t) = v_o - gt$, то есть на скорость тела в этот момент времени $t$ (найти его все же придется, решая квадратное уравнение). Находим $\Delta t$ в точке траектории $y=4{,}00\,\text{м}$, $t=0{,}55\,\text{с}$: \begin{equation} \Delta t \approx \frac{\Delta y}{v_o-gt} = \frac{0{,}01\,\text{м}}{10\,\text{м/с}-10\,\text{м/с$^2$} \cdot 0{,}55\,\text{c}} = 0{,}0022\,\text{с} \end{equation}
Но для точки $y=5{,}00\,\text{м}$, $t=1{,}00\,\text{с}$ такое рассуждение не подходит, так как скорость $\dot{y}(t)$ в ней равна нулю. Нам придется написать более точную формулу для $\Delta y$, это формула Тейлора второго порядка: \begin{equation} \Delta y \approx \dot{y}(t)\Delta t + \tfrac{1}{2}\ddot{y}(t)\Delta t^2 \end{equation} И тогда при нулевой первой производной промежуток времени можно найти, деля $\Delta y$ на половину второй производной $\tfrac{1}{2}\ddot{y}(t)=-\tfrac{1}{2}g$ и извлекая корень. Только за $\Delta y$ надо брать отрицательную величину, так как выше $y=5{,}00\,\text{м}$ уже не подняться. \begin{equation} \Delta t \approx \sqrt{\frac{\Delta y}{-\tfrac{1}{2}g}} = \sqrt{\frac{-0{,}01\,\text{м}}{\tfrac{1}{2}\cdot(-10\,\text{м/с$^2$})}} = 0{,}0447\,\text{с} \end{equation}
Вывод. Эта задача еще раз демонстрирует то, как гладкая функция задерживается в своей стационарной точке.
$\,$
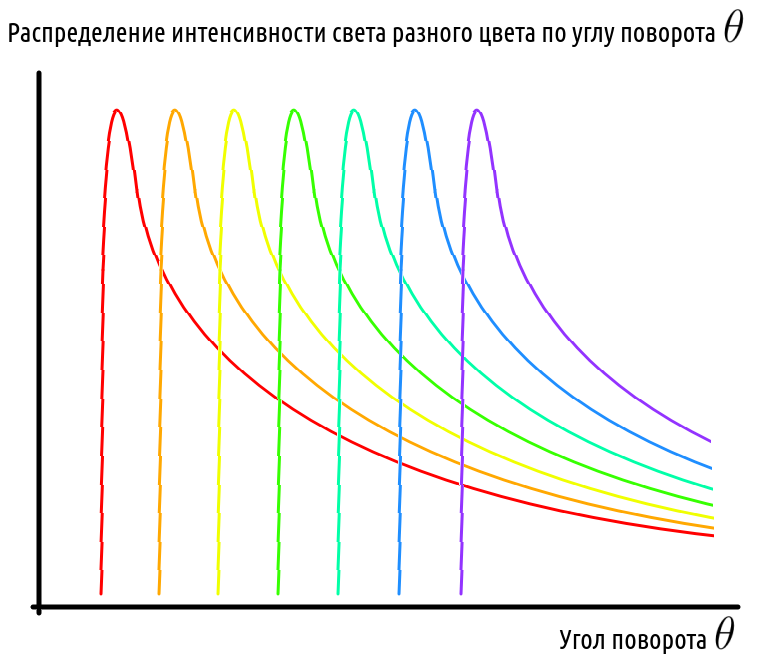
5. Дело в том, что посчитанные нами углы $\theta^*$ — это лишь пики в угловом распределении лучей. Свет не рассеивается под меньшими углами, но рассеивается под большими. Поэтому распределения для разных цветов накладываются друг на друга. Причем форма распределений такова, что красный цвет накладывается на все остальные, но на него ничто не накладывается. А на синий цвет накладываются голубой, зеленый, желтый, оранжевый и немножко красный. Поэтому синяя полоса радуги вовсе и не синяя. Если вы хотите увидеть настоящие спектральные цвета, посмотрите на дифракцию на DVD-диске.
$\,$
6. Обозначим углы как на картинке
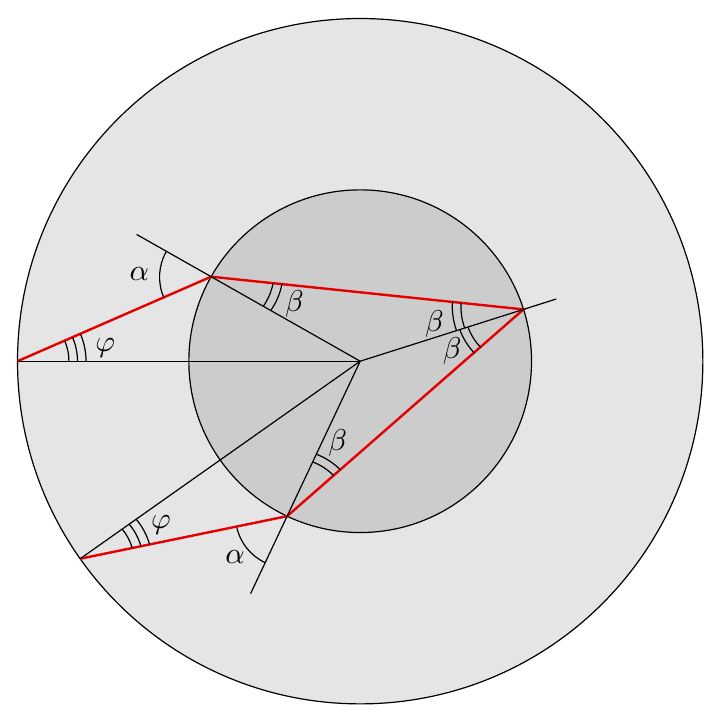
Угловое расстояние между началом (землятрясение) и концом сейсмического луча равно $\theta = 2\varphi-2\alpha+4\beta$. Углы $\alpha$ и $\beta$ связаны законом Снелла: \begin{equation} \sin\alpha = n\sin\beta \end{equation} A углы $\alpha$ и $\varphi$ связаны несложной геометрией. Расстояние от прямой, по которой начинает идти луч, до центра равно с одной тороны $R\sin\varphi$, а с другой стороны $r\sin\alpha$, где $R$ и $r$ — радиусы планеты и ее ядра.
Получается удобным выразить $\theta$ через $\alpha$ \begin{equation} \theta = -2\alpha + 2\mathrm{arcsin}\dfrac{\sin\alpha}{R/r} + 4\mathrm{arcsin}\dfrac{\sin\alpha}{n} \end{equation} По случайности в нашей задаче $n=R/r$ и равно $2$. Поэтому \begin{equation} \theta = -2\alpha + 6\mathrm{arcsin}\dfrac{\sin\alpha}{2} \end{equation} А дальше все стандартно \begin{equation} \alpha^* = \mathrm{arctg}\sqrt{\dfrac{5}{3}} \qquad \theta^* = 35^\circ \end{equation}
