Решения
1. Каков цвет неба в RGB? Считайте, что атмосфера слабо рассеивает свет.
Ответим на этот вопрос очень грубо. Возьмем три длины волны $\lambda$: красного, зеленого и синего спектральных цветов. Формула Релея говорит, что интенсивность рассеяния пропорциональна $\lambda^{-4}$. Поэтому возведем их в минус четвертую степень.
\begin{array}{c|c|c}
цвет & \lambda, мкм & \lambda^{-4}, мкм^{-4} \\
\hline
красный & 0{,}65 & 5{,}6 \\
зеленый & 0{,}55 & 10{,}9 \\
синий & 0{,}45 & 24{,}4 \
\end{array}
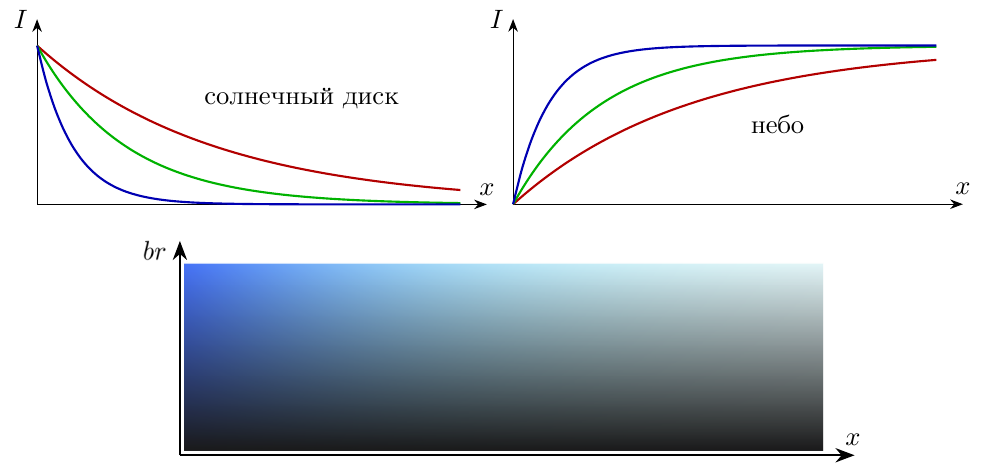
Их отношение примерно равно 1:2:5. Поэтому цвет (51,102,255) должен примерно соответсвовать цвету неба. На нижнем графике о слева сверху.
Для более точного решения нам потребуется закон Бугера–Ламберта–Бера, он говорит, что интенсивность луча света падает экспоненциально (то есть в геометрической прогрессии) по мере его распространения в поглощающей или рассеивающей среде: \begin{equation} I = I_o e^{-\gamma x} \end{equation} Коэффициенты $\gamma$ разные для разных цветов и относятся как 1:2:5 для красного, зеленого и синего. Поэтому интенсивности трех компонент прямых солнечных лучей падают экспоненциально, а интенсивности трех компонент света неба растут противоположенным образом. Итак, для разных значений толщины $x$ атмосферы и для разных значений яркости солнца мы получаем цвета на нижнем графике. Чем толще или плотнее атмосфера, чем больше в ней рассеивающих частиц, тем ее цвет менее насыщен, из-за того, что степень рассеяния синего света приближается к 100% и больше не растет, но растут степени рассеяния зеленого и красного. В пределе получается серое пасмурное небо, на котором солнечный диск совсем не виден.
2. Расстояние от точки наблюдения до полюсов диполя равно согласно теореме Пифагора $\sqrt{r^2+\ell^2/4}$. Поэтому электрические поля, создаваемые в этой точке равны $E_{\pm}=kq/(r^2+\ell^2/4)$. В горизонтальном направлении они компенсируют друг друга, а в вертикальном нет. Чтобы найти вертикальную компоненту пользуемся подобием закрашенных треугольников
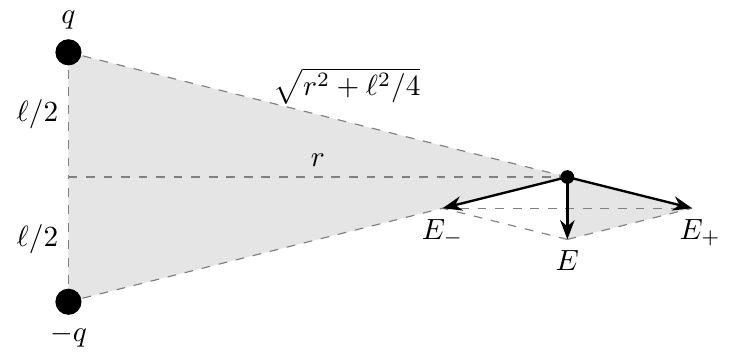
\begin{equation} \frac{E}{E_+} = \frac{\ell}{\sqrt{r^2+\ell^2/4}} \end{equation} \begin{equation} E=k\frac{q\ell}{(r^2+\ell^2/4)^{3/2}} \end{equation} На больших расстояниях $r\gg\ell$, поэтому $\ell$ в знаменателе можно пренебречь. Можно сказать, диполи любой формы и размера издалека выглядят примерно одиаково. Мы получаем формулу \begin{equation} E=k\frac{d}{r^3} \end{equation}
3. В теории Нильса Бора атом похож на солнечную систему, в которой электроны-планеты обращаются вокруг ядра-солнца. Радиус орбиты электрона в атоме водорода $r=0{,}5\cdot10^{-10}\,м$, а частота его обращения $\omega=4\cdot10^{16}\,с^{-1}$. Заряды элекрона и ядра по модулю равны $e=1{,}6\cdot10^{-19}\,\text{Кл}$. Найдите, с какой мощьностью должен излучать электрон. Соответствует ли это действительности? Константа Кулона $k=9\cdot10^9\,\text{Н$\cdot$м$^2$/Кл$^2$}$, скорость света $c=3\cdot10^8\,\text{м/с}$.
Дипольный момент атома Бора равен $d=er$ и вращается (как вектор) с частотой $\omega$. Подставляем в формулу мощности излучения: \begin{equation} P = \frac{ke^2r^2\omega^4}{c^3} = \frac{9\cdot10^9\cdot(1{,}6\cdot10^{-19})^2\cdot(0{,}5\cdot10^{-10})^2}{(3\cdot10^8)^3} \approx 10^{-7}\,(Вт) \end{equation} Эта огромнейшая мощность излучения. Ведь даже в одной столовой ложке воды число атомов водорода порядка $10^{23}$, но никакого излучения они не производят. Более того, если бы электрон действительно излучал с такой мощностью, то он отдал бы всю свою энергию за наносекунду и упал бы на ядро. Этого не происходит, следовательно электрон в атоме не излучает. Почему? Эта одна из главнейших проблем классической физики, решение которой было найдено лишь в квантовой механике.
4. Нам даны амплитуда волны $E$, ее частота $\omega$ и две константы входящие в уравнения Максвелла – это скорость света $c$ и константа Кулона $k$. Мы ищем плотность пока энергии $j$. Выпишем их размерности:
\begin{array}{c|c}
E & Н/Кл \\
\omega & с^{-1} \
c & м/с \
k & Н\,м^2/Кл^2 \
\hline
j & Вт/м^2 = Н/(м\,с) \\
\end{array}
Попробуем выразить $j$ как произведние $E,\omega,c,k$ в некоторых степенях
\begin{equation} j=E^\alpha \omega^\beta c^\gamma k^\delta \end{equation}
тогда для размерностей мы имеем уравнение
\begin{equation} Н/(м\,с)=(Н/Кл)^\alpha с^{-\beta} (м/с)^\gamma (Н\,м^2/Кл^2)^\delta \end{equation}
\begin{equation} Н\,м^{-1}\,с^{-1}\,Кл^0= Н^{\alpha+\delta} м^{\gamma+2\delta} с^{-\beta-\gamma} Кл^{-\alpha-2\delta} \end{equation}
\begin{equation}
\left\{\begin{array}{rrl}
Н: & 1=&\alpha+\delta \\
м: & -1=&\gamma+2\delta \
с: & -1=&-\beta-\gamma \
Кл: & 0=&-\alpha-2\delta \
\end{array}\right.
\end{equation}
Эта система уравнений имеет единственное решение
\begin{equation} \alpha=2 \qquad \beta=0 \qquad \gamma=1 \qquad \delta=-1 \end{equation}
поэтому с точностью до численного множителя
\begin{equation} j=\frac{E^2 c}{k} \end{equation}
А мощность излучения, падающего на частицу-мишень радиуса $R$, равна $P’=jR^2=\frac{E^2 c}{k}R^2$.
