Парадокс Браесса
Еще одна интересная и жизненная задача с неожиданным ответом. “Тише едешь, дальше будешь” - как говорится, и действительно, иногда выбор не самого быстрого пути, позволяет добраться до пункта назначения за кротчайшее время. Об этом парадокс Брайесса.
Представим себе большую группу автомобилистов, мечтающих добраться из пункта Start в пункт Finish. Сделать это можно двумя путями, один лежит через пункт A , другой лежит через пункт В. Дорога из Start в A прямая, а потому короткая, но очень узкая, на ней велика вероятность встать в пробку. Поэтому время \(t_{SA}(мин) \) , которое требуется, чтобы преодолеть этот участок пути, сильно зависит от числа людей \(T\), избравших именно эту дорогу. Скажем,
\[t_{SA}=T/100\]
То есть пустую эту дорогу можно преодолеть практически мгновенно, а вот в компании 4000 таких же автомобилистов только за 40 минут. Такая же пусть будет и дорога из B в Finish, \(t_{BF}=T/100\).
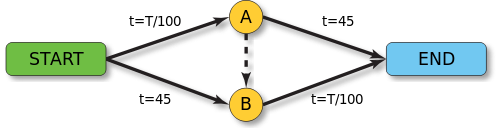
А вот дороги из A в Finish и из Start в B наоборот очень широкие, но очень длинные и плохого качества, поэтому на их преодоление необходимо потратить 45 минут независимо от того, сколько по ней едет машин: \(t_{AF}=t_{BS}=45\)
Вопрос первый: за сколько минут 4000 автомобилистов доберутся из пункта Start в пункт Finish?
Задача облегчается тем, что две дороги симметричны, а поэтому очевидно, что половина изберет путь через A, а половина поедет через B. Получается \(t=\frac{2000}{100}+45=65\). Час и пять минут.
Теперь представим, что не очень умное, но любящее нас градоначальство решило помочь автомобилистам и решить проблему пробок строительством супермегананоскоростной трассы A-B. К тому же пропускная способность новой дороги неограниченна, а потому \(t_{AB}=0\).
Вопрос второй: за сколько минут 4000 автомобилистов доберутся из пункта Start в пункт Finish теперь?
Путь в A займет в худшем случае 40 минут, а от туда рукой подать до B, до которого напрямую ехать 45 минут. Значит все поедут в А, потом мгновенно перемещаются в B, а потом в Finish. Итого получаем \(t=\frac{4000}{100}+0+\frac{4000}{100}=80\). Час двадцать! Куда делись 15 минут?
А эти 15 минут ушли на пробки, которые образовались из-за того, что все ломанулись на узкие дороги от Start до A и от B до Finish. Но что делать, таково равновесие Нэша, каждый делает то, что ему выгодно. Можно ли было этого избежать? Да, оптимальный вариант в данном случае полностью игнорировать новую дорогу и делать все по старинке: половина через A , половина через B. И это есть равновесие Парэто, потому как, если в данной ситуации кто-то захочет срезать и проехаться по новой дороге, то он затратит не 65 минут, а всего \(t=\frac{2000}{100}+0+\frac{2000}{100}=40\) минут, но зато все остальные 3999 автомобилистов почувствуют прибавку к времени в 0,01 минуты, что в сумме дает примерно 40 минут. Выгоду получает один, а издержки все. Ну точно так же, как когда кто-то ворует лампочку в подъезде.
Мораль сей басни вовсе не в том, что не нужно строить дороги, а в том что, во-первых, делать это надо с умом, а во-вторых, надо уметь договариваться о совместном использовании общих благ, тогда это использование будет оптимальным.
Почитать: книга А.В. Гасникова о транспортных потоках. Глава 1.3 посвящена транспортным парадоксам, в том числе конкретному примеру с городом Владивосток.
