Решения
1. Из полученной в видео формулы выражаем длину волны: \begin{equation} \lambda = \dfrac{d\,\Delta x}{L} = \dfrac{0{,}3\,\text{мм}\cdot7\,\text{мм}}{5\,\text{м}}=420\,\text{нм} \end{equation} Именно такое значение и именно по таким формулам получил сам Юнг для фиолетового света. Хотя, конечно, лазера у него не было. Он использовал белый свет, который в результате интерференции раслагался на спектральные составляющие.
2.a. Длина волны излучения антенн $\lambda=c/\nu$. Расстояние между областями конструктивной интерференции на высоте самолета $\Delta x = \lambda H/d$. Это расстояние самолет пролетает за время $T_\text{б}=\Delta x/v$. Это и есть период биений.
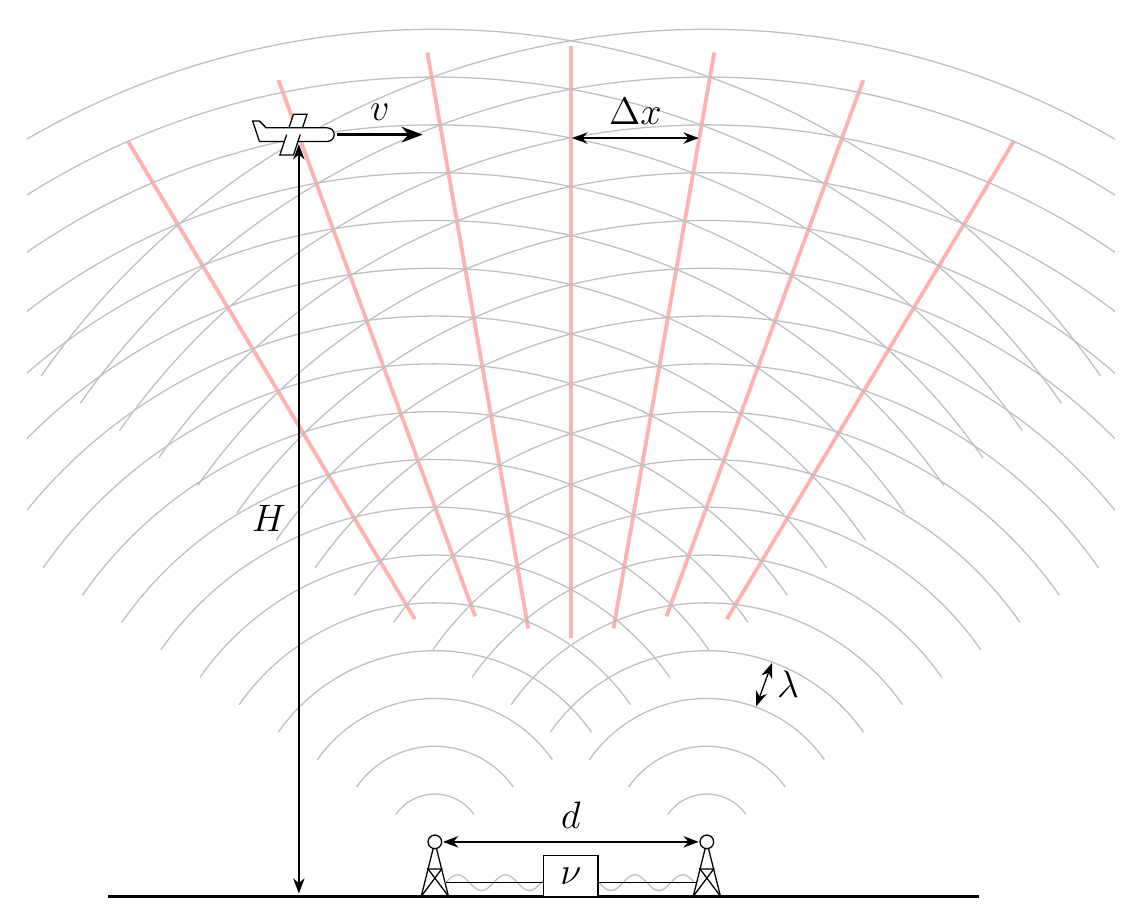
\begin{equation} T_\text{б} = \dfrac{\Delta x}{v} = \dfrac{\lambda H}{vd} = \dfrac{c H}{vd\nu} = \dfrac{300\,000\,\text{км/с}\cdot3\,\text{км}}{300\,\text{м/с}\cdot100\,\text{м}\cdot300\,\text{МГц}}=0{,}1\,\text{с} \end{equation}
2.b. Заметим аналогию с предыдущей задачей. Условие того, что волны дошедшие до антенн будут в синфазе ровно такое же, как условие того, что в предыдущей задаче самолет пролетал через область конструктивной интерференции. Поэтому решение полностью аналогично и формула, полученная в предыдущей задаче, верна и здесь.
\begin{equation} v = \dfrac{c H}{T_\text{б}d\nu} = 300\,\text{м/с} = 1080\,\text{км/ч} \end{equation}
3.a. Угол между гиперболами конструктивной интерференции определяется формулой $\sin\theta_n=n\lambda/d$. Поэтому при уменьшении длины волны, угол между гиперболами уменьшается, а их количество увеличивается.

3.b. В этом случае количество гипербол и угол между ними не меняется. Меняется кое-что другое. Так как два единственных параметра, входящих в задачу, $\lambda$ и $d$ имеют одинаковую размерность (метры) и уменьшаются в одинаковое число раз, то все расстояния врешинии задачи уменьшатся в такое же число раз. Это выглядит так, как будто мы, наблюдатели, удаляемся от картины.

4.a. Как мы упоминали в видео, энергетической характеристикой волн является интенсивность, которая пропорциональна квадрату амплитуды. Поэтому усредняем квадрат амплитуды
\begin{equation} \langle A^2 \rangle = 2a^2 (1+\langle\cos(kdx/L)\rangle) = 2a^2 \end{equation}
Среднее значение косинуса равно нулю. Поэтому средняя интенсивность двух интерферирующих волн оказывается ровно вдвое больше интенсивности одной волны. Энергия перераспределяется в пространстве, но сохраняется.
4.b. Складываем два вращающихся вектора длины $a_1$ и $a_2$, угол между которыми сохраняется равным $\Delta\varphi \approx kdx/L$. Очевидно, суммарный вектор вращается с той же угловой скоростью и сохраняет свою длину. Ее мы найдем через скалярное произведение:
\begin{equation} A^2 = (\vec{a_1}+\vec{a_2})^2 = a_1^2 + 2\vec{a_1}\vec{a_2} + a_2^2 = a_1^2+2a_1a_2\cos\Delta\phi + a_2^2 \end{equation}
Чем отличается этот случай от случая равных амплитуд? В областях деструктивной интерференции, там где $\cos\Delta\varphi=-1$, амплитуда света оказывается не нулевая. Она равна разности амплитуд слагаемых волн $A_{\min}^2=(a_1-a_2)^2$. Интерференционная картина получается менее контрастной.

При усреднении интенсивности косинус опять-таки обнуляется и получается
\begin{equation} \langle A^2 \rangle = a_1^2+2a_1a_2\langle\cos(kdx/L)\rangle + a_2^2 = a_1^2+a_2^2 \end{equation}
— сумма интенсивностей слагаемых волн. То есть энергия сохраняется.
4.c. Складываем три вектора длины $a$, углы между которыми $\Delta\varphi$ (между 1-м и 2-м и между 2-м и 3-м) и $2\Delta\varphi$ (между 1-м и 3-м). Опять-таки очевидно, что суммарный вектор вращается с той же скоростью и сохраняет свою длину. Ищем эту длину: \begin{equation} A^2 = (\vec{a_1}+\vec{a_2}+\vec{a_3})^2 = a_1^2+ a_2^2+ a_3^2 + 2\vec{a_1}\vec{a_2}+ 2\vec{a_1}\vec{a_3}+ 2\vec{a_2}\vec{a_3} = \end{equation} \begin{equation} =a^2+ a^2+ a^2 +2a^2\cos\Delta\phi +2a^2\cos2\Delta\phi +2a^2\cos\Delta\phi= \end{equation} \begin{equation} =a^2(3+4\cos\Delta\varphi+2\cos2\Delta\varphi) \end{equation}
График этой функции непросто построить вручную. Если только заметить, что $3+4\cos\Delta\varphi+2\cos2\Delta\varphi = (1+2\cos\Delta\varphi)^2$. Значит график выглядит так:

При усреднении интенсивности косинусы пропадают, а остается $\langle A^2\rangle = 3a^2$, что означает, что энергия и в этом случае сохраняется.
