Решения
1. Подставим в закон Снелла угол преломления равный $\beta=90^\circ$, и тогда получим $n\sin\alpha=1$, следовательно $\sin\alpha = \tfrac{1}{2}$, следовательно $\alpha=30^\circ$.
2. Как-то так
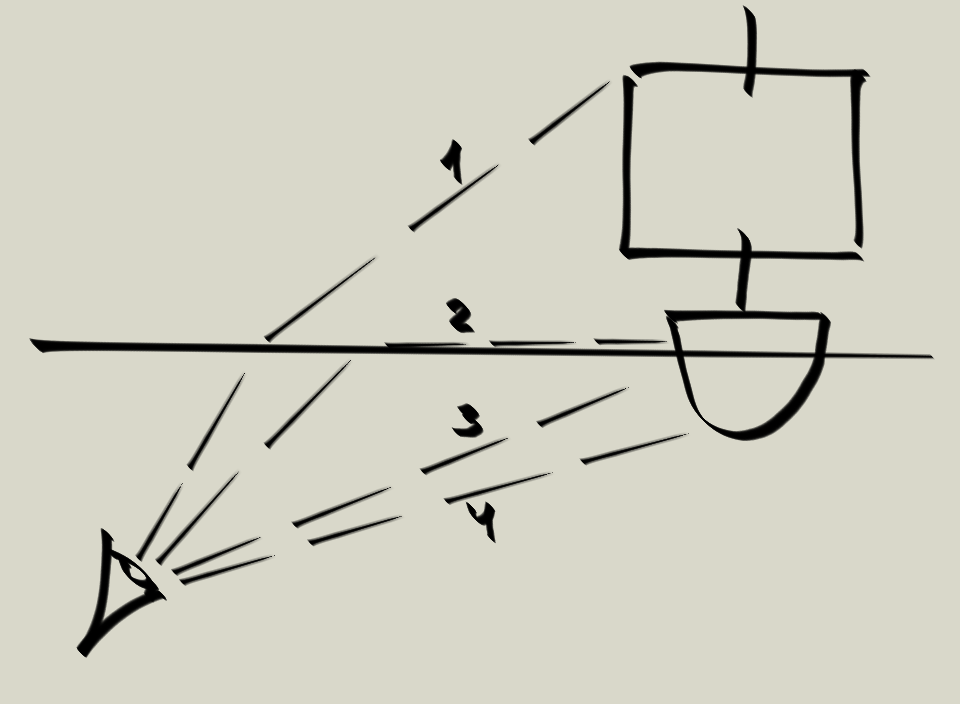
3. Нет, не образуют. На рисунке показан ход лучей. Лучи 2 и 3 идут от ватерлинии корабля, но луч 2 идет по воздуху почти вдоль поверхности воды, а луч 3 сразу идет под водой. Они попадают в глаз под разными углами, поэтому корабль как-бы разрывается на две части: надводная видна в промежутке 1-2, а подводная в промежутке 3-4.
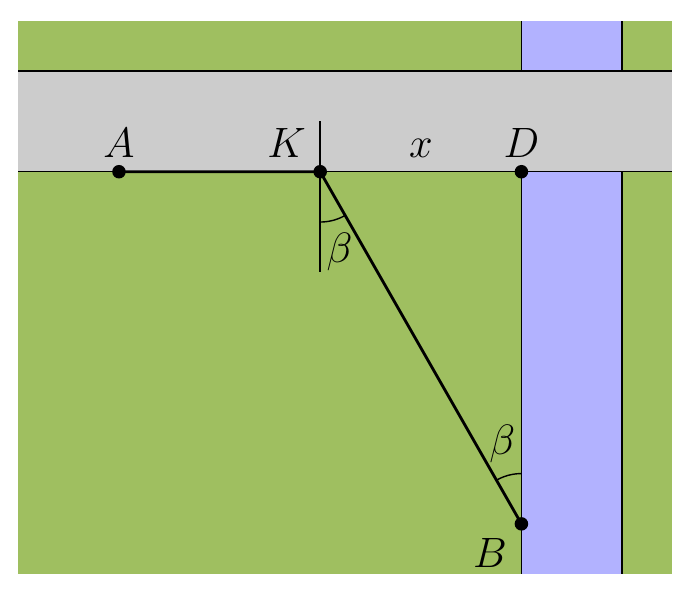
4. Действительно, закон преломления применим в этой задаче. Отношение скоростей по дороге и по полю равно $5:3$, поэтому задача аналогична преломлению света при прохождении из воздуха в среду с показателем преломления $n=5/3$. Причем падающий луч падает под прямым углом к нормали, следовательно синус угла преломления равен $\sin\beta=1/n=3/5$. Угол преломления $\beta$ — это угол в прямоугольном треугольнике $\triangle BKD$. Мы знаем катет $BD=36\,\text{м}$. Чтобы найти другой катет и гипотенузу, нужно знать косинус и тангенс угла $\beta$. Мы находим их исходя из основного тригонометрического тождества: $\cos\beta=4/5$, $\mathrm{tg}\beta=3/4$. Тогда $BK=45\,\text{м}$, $KD=27\,\text{м}$, и тогда $AK=15\,\text{м}$. Мы нашли положение точки $K$.
Решим задачу иначе, не прибегая к оптическим аналогиям. Пусть $x=KD$, тогда время пути может быть записано так \begin{equation} t(x)\quad=\quad \dfrac{AK}{1{,}5\,\text{м/с}}+\dfrac{KB}{0{,}9\,\text{м/с}}\quad=\quad \dfrac{AD-x}{1{,}5\,\text{м/с}}+\dfrac{\sqrt{BD^2+x^2}}{0{,}9\,\text{м/с}} \end{equation} Время $t$ является функцией от расстояния $x$. Чтобы найти минимум этой функции, согласно лемме Ферма необходимо найти те значения $x$, при которых производная функции $t$ равна нулю. Найдем ее \begin{equation} t’(x)\quad=\quad \dfrac{-1}{1{,}5\,\text{м/с}}+\dfrac{x}{0{,}9\,\text{м/с}\,\sqrt{BD^2+x^2}} \end{equation} Тогда получаем уравнение \begin{equation} 0{,}9\,\sqrt{BD^2+x^2} = 1{,}5\, x \end{equation} откуда $x=\tfrac{3}{4}BD=27\,\text{м}$. Подставим теперь в функцию $t(x)$ значения \begin{equation} t(27\,\text{м})=60\,\text{с} \end{equation} \begin{equation} t(27\,\text{м}+3\,\text{м})=60{,}07\,\text{с} \end{equation} \begin{equation} t(27\,\text{м}-3\,\text{м})=60{,}07\,\text{с} \end{equation} Мы видим, что небольшие изменения положения точки $K$ приводят пусть и к незначительным, но увеличениям времени пути.
5. Да. Наша атмосфера неоднородна, с высотой падает ее плотность и, как следствие, падает показатель преломления, то есть возрастает скорость света. Свет выбирает быстрейший путь, и этим путем является не прямая, а выпуклая вверх линия. Это аналогично полному внутреннему отражения, только плавное. Но это не опровергает доказательство шарообразности Земли, а наоборот усиливает его. Искривление лучей света позволяет видеть корабль даже чуть-чуть дольше, когда он уже геометрически скрылся за горизонт.
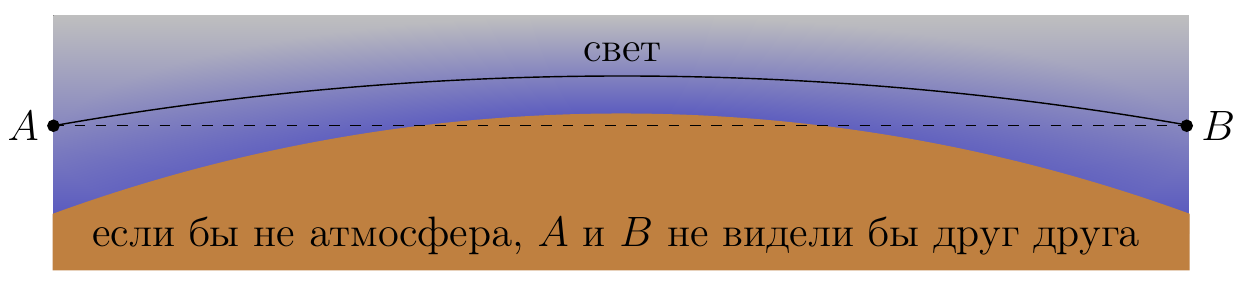
6. Нет, не может. Максимальный угол преломления при переходе из воздуха в стекло достигался бы при угле падения $\alpha=90^\circ$ и равен $\beta_{max}=\arcsin\tfrac{1}{n}$ (он же и есть угол полного внутреннего отражения). Поэтому \begin{equation} \beta < \arcsin\dfrac{1}{n} = \arcsin\dfrac{2}{3} < \arcsin\dfrac{1}{\sqrt{2}} = 45^\circ \end{equation} Мы воспользовались тем, что функция арксинус возрастающая, а $\tfrac{2}{3}<\tfrac{1}{\sqrt{2}}$. Если бы луч мог пройти через стеклянный куб, то сумма углов $\beta_1$ (преломления на первой грани) и $\beta_2$ (падения на вторую грань) равнялась бы прямому углу. Но это невозможно, так как каждый из них меньше $45^\circ$.
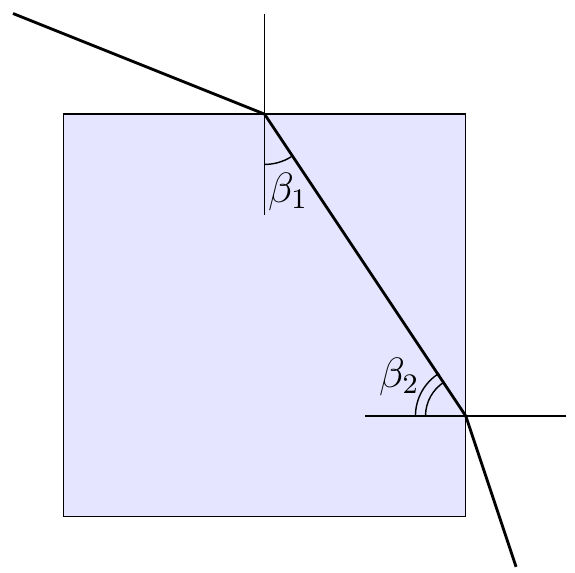
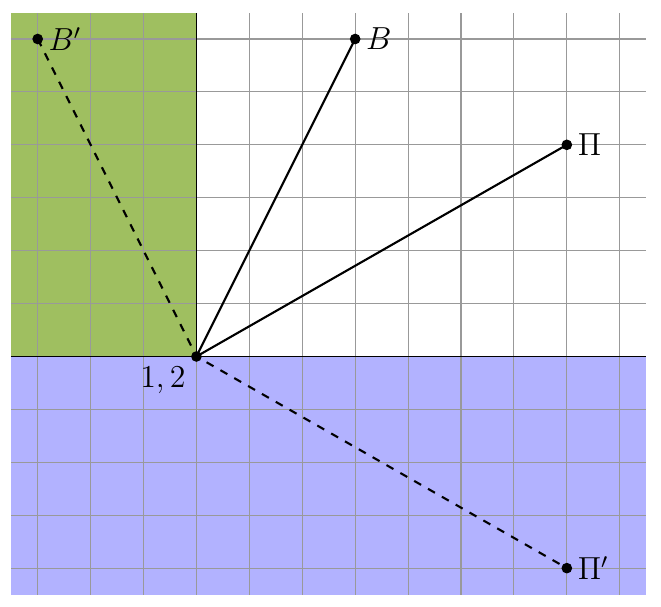
7. Чтобы найти кратчайший путь Винни-Пуха, предположим, что мы его уже нашли. Отразим часть пути от дома Винни-Пуха $B$ до точки поедания малины в лесу $1$ относительно края леса, а часть пути от точки питья воды $2$ до дома Пяточка $\Pi$ относительно берега реки. Так мы получим ломаную $B’12\Pi’$, длина которой равна длине настоящего пути Винни-Пуха $B12\Pi$.
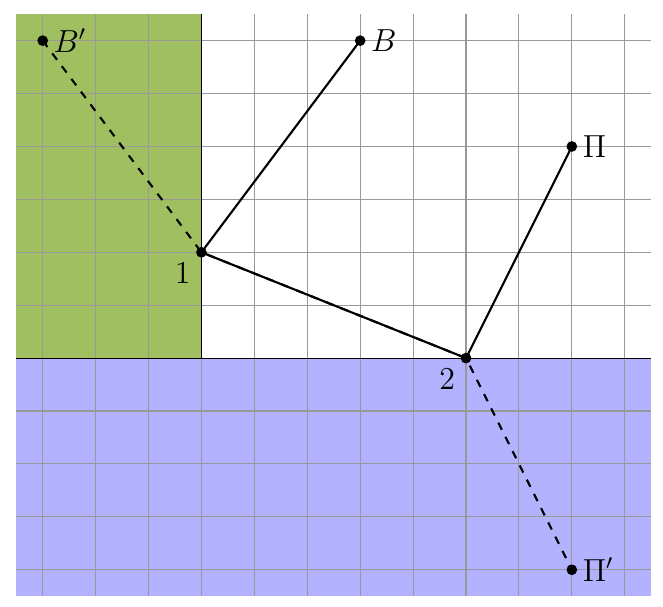
Самая короткая ломаная — это прямая, поэтому точки $1$ и $2$ должны лежать на прямой $B’\Pi’$. Так мы находим кратчайший путь от Винни-Пуха до Пяточка. Обратите внимание, углы падения пути Винни-Пуха на границу леса и реки равны углам отражения. Это хорошая иллюстрация того, как принцип наименьшего времени Ферма приводит к закону отражения света.
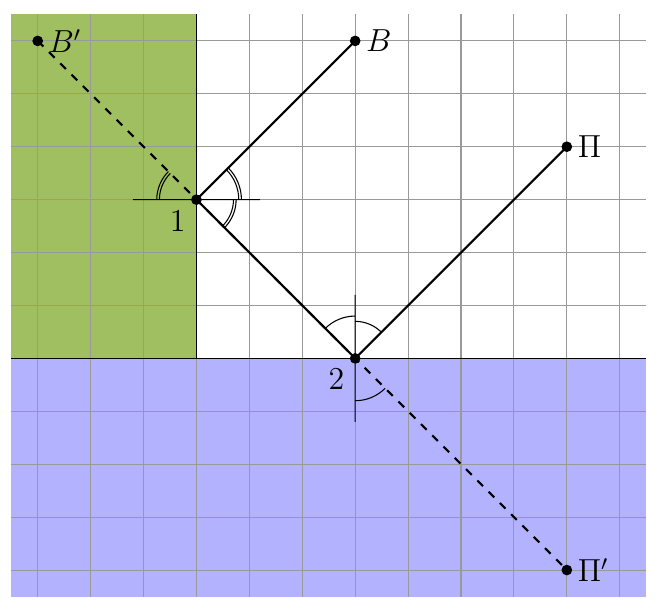
8. Теперь с уменьшением скорости Винни-Пуха между едой и питьем мы получаем задачу аналогичную прохождению света через две смежные грани стеклянного куба. Мы уже знаем, что свет не может так распространяться из-за явления полного внутреннего отражения. Дело в том, что свет так медленно распространяется в стекле, что быстрее будет пойти в обход, через ребро куба. То же и с Винни-Пухом, он предпочтет поесть и попить в одной точке.