Еще немного о вращении книги
Почему же все-таки возникает неустойчивость? Ведь то, что не запрещено законами сохранения, далеко не факт что произойдет. Давайте разберемся в этом. Мы решаем вот такое простое уравнение. \(\dot{L}=0\) Момент импульса это есть произведение тензора инерции и вектора угловой скорости, поэтому \(\dot{J}\omega +J\dot{\omega }=0\) Чему равна производная тензора инерции? Если вспомнить, при вращении тела, произвольный вектор, соединяющий две его точки, меняется по закону \(\dot{r}=\omega \times r\). А тензор инерции, как всякий тензор, меняется как два «слипшихся» вектора. То есть омегу на него нужно умножить дважды, сначала на один вектор, а потом на второй, и когда будем умножать на второй, лучше зайти справа, при этом изменив знак. \(\dot{J}=\omega \times J-J\times \omega\) Все это можно было бы записать строже, используя индексные обозначения, но это было бы весьма громоздко. Далее используем тот факт, что встреча двух одинаковых векторов в смешанном произведении обнуляет его, а значит \([J\times \omega ]\omega =0\). И получаем вот такое уравнение для производной угловой скорости. \(\dot{\omega }=J^{-1}[\omega \times J]\omega\) Теперь возьмем конкретный случай, когда тензор инерции и угловая скорость имеют такой вид \(J=\left(\begin{array}{ccc} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & c\end{array}\right) ,\ \ \ \ \omega =\left(\begin{array}{c} x \\ \omega \\ z\end{array}\right)\) Если x и z равны нулю, то это просто вращение вокруг оси с моментом инерции b. Рассмотрим небольшое отклонение оси, то есть пусть x и z очень малы. Я не буду писать все выкладки, получается следующее \(\dot{\omega }=\left(\begin{array}{c} \frac{c-b}{a}z\omega \\ \frac{a-c}{b}xz \\ \frac{b-a}{c}x\omega\end{array}\right)\) В этой формуле интересно то, что производная x-компоненты скорости пропорциональна ее z-компоненте и наоборот. Рассмотрим их в отдельности в виде системы дифуров. Если соотношение между моментами инерции \(a>b>c\), то знаки в системе будет такие \(\begin{cases} \dot{x}\simeq -z \ \dot{z}\simeq -x\end{cases}\) Кто работал с такими системами, сразу видит здесь седло. Кто не работал пусть посмотрит на карнтинку с векторным полем производной от (x,z).
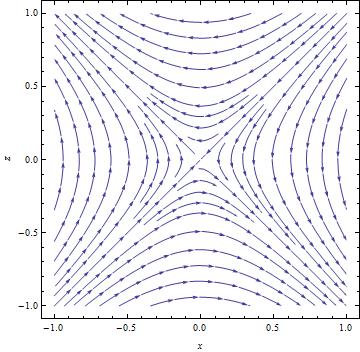
Видно, что если система немного отклонится от положения равновесия, то ее унесет далеко и надолго, а это и есть неустойчивость.
А если моменты инерции такие \(b>a>c\), то знаки в уравнении будут такие \(\begin{cases} \dot{x}\simeq -z \ \dot{z}\simeq x\end{cases}\) И мы получаем фокус. То есть система немного отклонившись, будет дальше двигаться по окружности, не удаляясь от первоначального положения.
